Blog

Digital loudspeaker controllers are the heart of every modern PA-system. Controllers assign the matching signal to every speaker, balance inconsistencies in the frequency range and protect the system from overload.

Loudspeaker controllers normally consist of these three important components:

– the hardware including the connectors and interfaces, the transducers, the operating elements and the housing.

– the firmware includes algorithms for signal processing, i.e. equalizers, crossovers, limiters and delays.

– the software providing a graphical surface on the user’s computer for adjusting all controller functions and settings and manage complete setups.
Before the digital era, most audio controllers were not much more than active crossovers, they did not have several features like preset memories and password protection. Some of these controllers did not even have variable crossover frequencies, the only possibility was to exchange one crossover by another. These controllers were mainly designed for one special speaker-system and could not be used very flexibly.

In the meantime, powerful digital management systems are also affordable for amateurs and semi-professional users. Subwoofers are only seldom operated via passive crossovers, but rather separated from the hi/mid speakers via controllers. The “bad thing” about the digital revolution is that many users are overwhelmed by the quantity of functions.

Due to the limited space of this article, we cannot discuss every part of a modern audio controller but hope to supply the reader with some important basic facts in order to handle his digital controller.

Controllers are installed after the mixer, or if available after the graphic equalizer in the signal chain. In this case, the equalizer is not for correcting the frequencies in the speakers, but adjusting the PA-system to the acoustic characteristics of the venue.

The first important task of a controller is adjusting the signal levels. It is common practice to have the power amplifiers at full gain controls in order to prevent them from manipulation because amptown is mostly far away from the sound engineer. Furthermore, the levels of different speaker ways of an actively separated system must be balanced to a matching ratio.

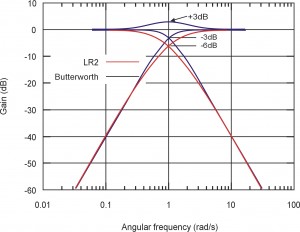Before that, the incoming sum signal has to be separated to the different speaker sizes. For doing so, most controllers offer different filter types and slopes. The filter characteristics mostly differ in their way of behaving at their specified working field. While butterworth filters lower the level at the crossover frequency by 3 dB, Linkwitz-Riley filters, which are based on a number of butterworth filters, lower the level by 6 dB. The advantage of this characteristics is the constant level in the crossover area from one frequency band to another. In order to realize such constant level with butterworth filters, the working area of the first frequency band’s lowpass filter and the second band’s highpass filter have to be exactly calculated and then separated. When using Linkwitz-Riley filters, the upper and lower crossover frequency of consecutive frequency bands can have the same frequency. The mostly available Bessel filters have a less strong bended amplitude compared with Butterworth filters, but a better frequency response and constant group delays. Common abbreviations for Butterworth is BW, for Linkwith-Riley L-R (not to be mixed up with left/right).

The Butterworth and Bessel filters are mostly available with 6, 12, 18 and 24 slopes, sometimes also 36 and/or 48 dB per octave. Linkwitz-Riley filters are only available in 12 dB per octave, while 24 dB is one of the mostly used slopes for crossover frequencies. Slope means how fast the amplitude is lowered after reaching the crossover frequency. For a lowpass filter with a 12 dB per octave slope and a crossover frequency of 1 KHz, the amplitudee at 2 kHz is 12 dB lower as at the crossover frequency (frequency doubling equals one octave). For a Butterworth filter, this is –15 dB, for a Linkwitz-Riley filter this is –18 dB. In theory, filters with quasi infinite slope were also possible, but this would hamper the phase of the signal and thus the sound very much.

So far for part one of digital loudspeaker management. The next part covers equalizers, delay functions, limiter and so on – stay tuned, it’s worth it!